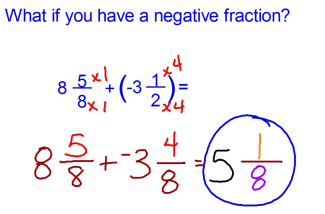Week of Dec. 15th

The week before Christmas Break, it is hard to believe one semester is almost over.  This week we will continue discussing the four parts of algebra that we have been learning about:  model, expression, t-chart, and graph.  What we know so far is, if given the model or the expression, we can evaluate a t-chart and graph the coordinates that the t-chart gives us.  This week we go the other way.  I will give the students the graph or the t-chart and they are to find the other missing parts.  We will do this lesson on Tuesday.  Monday we will be taking a Common Assessment over the Algebra that we have been studying

Here is a example of BBOA or the Building Blocks of Algebra.

Wednesday we will begin looking at the parts of BBOA using the Graphing Calculator.

Thursday and Friday we will be making icosahedrons as a Christmas Ornament project.  An icosahedron is a 20 faced polyhedron where each face is an equilateral triangle.

Students can bring Christmas cards if they would like to make their icosahedron or they will use the card stock they I have.

Friday, the students will be released at 1:00.  We will have a modified schedule that day.

December 19th – Early Release Bell Schedule

1st pd -- 7:45-8:15

2nd pd -- 8:19-8:49

3rd pd – 8:53-9:23

5th pd – 9:27-9:57

6th pd – 10:01-10:31

7th pd – 10:34-11:04

4th pd – 11:08-1:00

**Lunch Schedules**

A lunch – 11:08-11:38

B lunch – 11:44-12:14

C lunch – 12:20-12:50

I hope everyone has a wonderful weekend.

Bonus Question of the week:

Braden is downloading a file. The size of the file is 3,200 KB. It takes 3 minutes to download the first 1,200 KB of the file. If the file continues downloading at the same rate, how many more minutes will it take to finish downloading?

Copy the question, work and answer it with its correct label, and turn it in by Thursday, Dec. 18th for 10 Bonus points.

Week of Dec. 8th

Monday, we will again be looking at patterns, but they will be patterns found within a T-Chart.  The patterns will help us find the expression that created the T-Chart.  Linear expressions come in the form or y=mx + b where m refers to the slope and b refers to the y-intercept.  Slope is where determines the steepness of the graph.  The y-intercept is the point where the graph crosses the y-axis.  We will learn how to find these values in the T-Chart.

To review this lesson you can watch the video at http://goo.gl/ufVTt6.

Tuesday, I will be out so the students will complete the assignment over Monday's lesson.

Wednesday, we will be finding the expression from a graph.  The students will learn the proper order to write the points in a T-Chart and then find the expression.  They will also learn how to find the slope and y-intercept straight from the graph.

Thursday and Friday we will be reviewing for a our test on Friday.  I will post the review on my website.

Week of Dec. 1st

This week we have begun a new unit on Algebraic thinking.  There are connections that have to be made when beginning Algebra.  There is a connection between a physical model, an algebraic expressions, a t-chart, and a graph.

We started Monday by learning how to translate Language Arts sentences in to algebraic expressions and algebraic expressions back to LA sentences.

Examples:

5 more than t                           t + 5

6 less than 5 times g                5g - 6

y minus 8, times 4                   4(y - 8)

Also on Monday we evaluated expressions for a given value.

Examples:

Evaluate 4x + 3y for x = 3 and y = -2

4x + 3y
4(3) + 3(-2)
12 + -6
     6

Tuesday, we looked at numerical patterns.  Students were to use inductive reasoning to determine the next three values in a pattern.

Examples:

Pattern:  1, 3, 4, 6, 7, 9, 10, ...  _____, ______, ______

Students were to determine from the list how to go from one number to the next.  In this pattern you add 2 add 1.  So the next three numbers are 12, 13, 15.

Wednesday, we evaluated expressions using T-Charts.  Each expression we work with in the 7th grade is linear.  So when we evaluate the expression using a T-Chart they are able to make the connection with patterns.  Each expression has a consistent way to find the next number in the sequence.

Example:

Thursday, the students found out that the T-Chart actually created a set of coordinates for a coordinate plane or graph.  So we reviewed the parts of a graph and then graphed our T-Charts.

Example:

Friday, we put it all together by discussing the 4 parts of algebra that need to be connected.  We called it BBOA or the Building Blocks of Algebra which are the physical model, the expression, the T-Chart, and the graph.

Example:

Turkey Math

The Friday before Thanksgiving break we did a reflective activity called "Turkey Math."  Yes, in 7th grade students still like to cut and color.  I had the students write 7 math problems over topics that we have covered this year and put them on the feathers of the turkey.  The students then colored their turkeys and cut them out and put them together.  Here are some pictures.

Week of Nov. 17th

It is hard to believe we are one week away from Thanksgiving Break.  This year is going by so fast.  This week we will finish up our lessons on proportions by discussing Similar Figures.  This does not mean we will no longer use proportions, we will use them all year.  We will have that lesson on Similar Figures Monday.

Similar Figures are figures that meet the following conditions:
- The figures are the same shape but not the same size,
- Corresponding angles must be equal, and
- Most importantly, corresponding sides must be proportional.

Tuesday and Wednesday we will be working through pathways it Think Through Math.

Think Through Math is computer program (website) that personalizes learning for each student.

Thursday and Friday we will be working on some holiday related activities.

Bonus Question of the Week

Evaluate the following expression:

Copy the problem on your paper and solve.  Turn it in by Friday, Nov. 21st for 10 Bonus points.

Week of November 10 - 14

This week we will continue our lessons over proportions by discussing percent of change and similar figures.  There are two types of percent of change, percent of increase and percent of decrease.  Percent of change is found by dividing the amount of change in the situation by the original number.

Example:  Sam's grade during the 1st six weeks was an 85.  The 2nd six weeks he had a 92.  What was the percent of change from the 1st six weeks to the 2nd six weeks?

percent of change = 92 - 85   =     7    =  0.0823... x 100 = 8.2%
                                   85             85

To convert the number to a percent you multiply it by 100.

Wednesday, we will complete a test review for our first test of the 3rd six weeks and finish the week with a Common Assessment over Proportions and Percents.

Bonus Question for the Week

A real estate agent received a commission of $9375 on the sale of a home. If the commission
represents 7 1/2% of the selling price, how much did the house sell for?

Copy the problem, work it, and turn it in by Friday, November 14th for 10 Bonus points.

Percent Proportion

We ended last week by discussing the Percent Proportion.  The percent proportion is a tool you can use for all percent problems.  It is

   %    =   part  
 100       whole

The percent sign, part, and whole are all places where you plug in information from a problem.

There are 3 types of percent problems.  Problems where the % is missing, the part is missing, and the whole amount is missing.  Here are 3 examples:

What is 25% of 80?

20 is what percent of 80?

20 is 25% of what number?

Each of these problems can be solved by using the percent proportion.

Problem 1   25   =    x         Problem 2    x    =   20         Problem 3    25   =   20  
                  100       80                          100       80                           100        x

To solve each problem you cross multiply and divide by the value with the variable.

Problem 1    25   =    x   
                   100       80

                 100 x  =  25 (80)
                 100x  =  2000
                  100        100

                       x = 20

All 3 forms of the percent problems are solved the same way.

Most problems don't look like the examples.  They look more like this one:

The Incredible Chocolate Chip Company has discovered that 36 out of 400
chocolate chip cookies do not contain enough chocolate chips. What percent of
the chocolate chip cookies do not have enough chips?

In this problem we are looking for the percent so it will be like problem 2.

   x    =   36  
 100      400

400x = 3600
400       400

   x = 9%

For more information click here.

Ratio, Rate, Unit Rate, and Proportions

This past week we have been discussing how to simplify a ratio, and to identify a rate, how to find a unit rate, and how to find the missing value in a proportion.

A ratio is a comparison of 2 like quantities.  Ratios need to be in simplest form and they can be written 3 different ways.

Example:


This ratio can be written as 1:3, 1 to 3, or as a fraction 1/3.

A rate is a ratio that compares quantities of different units.
A unit rate is a comparison of a quantity to 1.

Example:

Unit rates become very important when doing price comparison.  We always want to get the best buy.

Example:

    

Which flash drive is the best buy?

5.99/8 = $0.75 per GB                                                         24.95/64 = $0.39

The 64 GB hard drive, according to price, is the better flash drive.

A proportion states that two ratios that are equal to each other.  To solve a proportion you find the cross products and solve for the missing variable by dividing.

Example:

Images from Google.

Week of Oct. 27th

This week we are going to try using our digital textbook to review and learn about ratios, unit rates, and proportions.

Monday - We will review the definition of a ratio, find equivalent ratios, and simplify ratios with different units.  This information can be found in Chapter 6 Section 1 of the digital textbook.  If you can not remember how to log in to the book click here.

Tuesday - We will find unit rates and use them to find other equivalents.  We will be discussing unit cost, price comparison, better buy, etc.  Our lesson will be Chapter 6 Section 2 in our digital textbook

Wednesday - We will learn to solve proportions.  We will solve them like an equation.  We will also have our 3rd Quiz over our Fraction to Decimal Equivalents.

Thursday - We will complete a hallway activity in groups over unit rate and proportions.  This activity will test the students ability to determine items that are a better buy.

Friday - Parent/Teacher Conference Day - Holiday for Students
If you would like to come and discuss how your child is doing in class please send me an email with a time you would like to come visit and I will schedule you into a slot around that time.  If your child seems to be doing fine you do not have to come unless you just want to.

Also, remember Monday, Nov. 3rd is a Teacher Staff Development day so it is also a Student Holiday.

Simple Interest

Today we learned how to calculate Simple Interest.  Simple interest is easy to calculate.  You use the formula I=Prt where I stands for Interest, P = principal (the amount of money you start with), r = rate (the percentage of interest that is used on the money), and t = time (that amount of time the money is earning interest).

Example:  I = _____, P = $1500, r = 5%, t = 3 years

          I = Prt
          I = 1500 x 0.05 x 3
          I = $225

Example:  I = $500, P = $2100, r = _____ , t = 4 years

          I = Prt
          500 = 2100 x r x 4
          500 = 8400 r

           500  =   8400 r 
          8400       8400

             r = 0.059...
             r = 5.95%

Just plug the information in to the equation and solve.

Week of Oct. 20th

This week is the middle of the 2nd six weeks.  Schools seems to be going quickly.  This week might be a long week for some though, we will be having 2 assessments this week.

Monday - Simple Interest

- This lesson will be an application of 1-Step equations.  Simple Interest can be figured using I=PRT (Interest = Principle x Rate x Time).

- Also, any student that did not perform satisfactorily on Test 2-1 will be taking a retest. 

Tuesday - Common Assessment

- We will be taking our first Common Assessment which will cover equations, inequalities, percents, and simple interest.

Wednesday - Test 2-2 Review

- We will review our unit test over equations and inequalities.

Thursday - Test 2-2

- Students will take their second test of the six weeks.

Friday - Begin creating a Digital Portfolio

- Portfolio's are becoming more and more necessary to use as part of a college application.  It is a collection of works by the student that demonstrates student growth.

This week is Homecoming and each day there is a way to show your spirit.

Bonus Problem of the Week

Jenna invests $13,000 into separate bank accounts, one earning 6% simple interest and the other earning 3% simple interest. If at the end of one year she earns $682.50 in interest, how much did she invest in each account?

Copy the problem, solve, and turn in by Friday, Oct. 24th for 15 Bonus Points.

2-Step Equations

Thursday and Friday we learned how to solve 2-Step Equations.  We began by reviewing the two types of 1-step equations:  equations with addition and subtraction, and equations with multiplication and division.

Our main goal in solving equations is to get the variable by itself, or isolate the variable.  With addition problems you add the opposite, with subtraction you change the subtraction sign to addition and the next number to its opposite then you add the opposite.

              x + 6 = -4                                           x - 8 = 4
    x + 6 + (-6) = -4 + (-6)                            x + (-8) = 4
                    x = -10                              x + (-8) + 8 = 4 + 8
                                                                              x = 12

With equations involving multiplication and division you do the opposite operation to isolate the variable.

             4x = 24                                  x    =  -3
                                                           5
            4x  =  24 
             4        4                                 5 x   =  -3 (5)
                x = 6                                   5
                                                               x = -15

With 2-Step equations you have both of the steps in the same problem.  To solve a 2-step equation you reverse the order of operations.  The last thing you did to solve an order of operation problem is add/subtract to the first thing you undo in an equation is add/subtract.

              2x + 6 = -10                                                     m  - 5 = 3
    2x + 6 + (-6) = -10 + (-6)                                           3
                     2x = -16                                         m  + (-5) + 5 = 3 + 5
                                                                            3
                     2x  =  -16                                                      m   =  8
                      2         2                                                        3
                       x = -8
                                                                                     (3)  m  = 8 (3)
                                                                                            3

                                                                                             m = 24

Graphing Inequalities

Today we began inequalities.  An inequality says that two quantities are not equal. Click on inequality for more explanation.

We learned how to write an inequality to represent a situation such as:

Situation:  My classroom can hold no more than 30 students.
Inequality:   s < 30   The number of students can be less than or equal to 30.

Situation:  The waiting room has at least 15 people in it.
Inequality:   p > 15    The number of people in the waiting room is 15 or more people.

We also learned how to graph inequalities.  If the inequality is < or > then you would use an open circle because the solution does not include the value.  If the inequality is < or > then you would use a closed circle because the solution does include the value.

Here are some examples.

Tuesday we will solve 1-step inequalities and graph the solutions.

Images used from Google images.

Week of Oct. 13th

We have now completed 7 weeks of school, that is hard to believe.  This week we will learn about 1-step inequalities and 2-step equations.  Last week we began with 1-step equations with addition and subtraction then multiplication and division.  This week we will put both steps together.

Monday and Tuesday:  1-Step Inequalities
- We will begin by learning how to graph inequalities and then we will solve them.

Wednesday and Thursday:  Solve 2-Step Equations
- We will put our knowledge of 1-step equations with add/subtract and multiply/divide and put them together.

Friday:  Right now the plan is to create equations and inequalities from word problems and solve them.  This plan may change.


Bonus Question of the Week:
A physical therapist earns $87,000 annually. The therapist owes 6.2% of her earned wages for social security tax. She also owes 1.45% of her earned wages for Medicare tax.

What are the physical therapist's total payroll deductions for social security tax and for Medicare tax for the year?

Copy the problem, solve, and turn in by Friday, Oct. 17th for 10 extra bonus points.

Solving 1-Step Equations

In order understand 1-step equations you need to understand four vocabulary words:
Variable, Constant, Expression, and Equation.  Click on the word for its definition.

1-Step Equations are equations that require only one step to solve.  For all equations we have one goal in mind and that is to get the variable by itself.  For an equation involving addition you add the opposite of the number with the variable to get the variable by itself.  If the equation involves subtraction you LCO the problem and then add the opposite.  For equations involving multiplication and division you don't add the opposite but you do the opposite.

Examples:

Addition:
          x + 5 = 9
x + 5 + (-5) = 9 + (-5)    Add the opposite
                x = 4

Subtraction:
             m - 8 = -4
        m + (-8) = -4     LCO
  m + (-8) + 8 = -4 + 8     Add the opposite
                   m = 4

Multiplication:
       4g = 12

      4g  =  12     Since you have a multiply by 4 you do a divide by 4 to get the variable by itself.
       4        4
         g = 3

Division:
       h  = -7
       5

 (5)  h  = -7 (5)   Since you have a divide by 5 you do a multiply by 5 to get the variable by itself.
       5

        h = -35

October 3, 2014 - Sales Tax, Discount, and Tip

Thursday, we discussed how to find percent of a number, today we learned how to apply what we learned.

Sales Tax - a percentage of the total purchase that is added to your purchase.  In Huntsville our tax rate is 8.25% of your purchase.

Example:
Ms. Acton spent $205.60 at Target. If the sales tax is 6%, what was her final bill?

The first thing you do is determine the percent question being asked:

What is 6% of $205.60?

.06 x $205.60 = 12.336  We round this amount to the nearest cent, $12.34 and add that amount to the amount Ms. Acton spent.

$205.60 + $12.34 = $217.94

Her final bill was $217.94.

Discount - a percentage of the total purchase that is subtracted from your purchase.

Example:
Macy's is having a one-day 35% off special. If Sara bought $124.50 worth of items, what would the final bill total after applying the discount of 35%?

So what is the percent question:  What is 35% of $124.50?

0.35 x $124.50 = 43.575 = $43.58 is the amount of discount.  You subtract this amount from $124.50.

$124.50 - $43.58 = $80.92   Sara's final bill is $80.92.

Tip (gratuity) - a percentage of your bill at a restaurant that you leave for the wait staff.

Example:

The Kerwoods went out to eat at Chille's. If there bill was $58.65 and they gave their server a 15% tip, how much did they pay altogether?

The question is What is 15% of $58.65?

0.15 x $58.65 = 8.7975 = $8.80 is the amount of tip the Kerwoods should leave.  Now the question asks how much did they pay all together?  So you need to add the bill total and the tip together.

$58.65 + $8.80 = $67.45 is the total amount spent by the Kerwood family at Chille's.

October 2, 2014 - Percent of a Number

Today, in class we learned how to calculate percent of a number.  This topic, in my opinion, is one of the most important topics a student can learn.  Percent of a number is calculated for us all the time:  sales tax, discount, a tip at a restaurant, interest rates etc.

Percent of a number questions come in the form of questions like:   What is 40% of 80?

I discuss with the students that this is a Language Arts style question.  We need to translate this into a mathematical question.

  What   is 40% of 80?         translate into
______ = 40%  x  80

The What is a blank, is means =, and of means multiply.  We are using calculators in class so they multiply 40% by 80.  There is only one problem, our calculator, the TI-83, does not have a percent key.  TI assumes that if you are smart enough to use their calculator you are smart enough to know how to type a percent into the calculator.  All you do is change the percent into a decimal by moving the decimal 2 places to the left.

_ 32    = .4 x 80

Here are a couple more examples.

What is 25% of 75?   -   .25 x 75 = 18.75
What is 15% of $120?     -     .15 x 120 = $18
What is 0.5% of 12?     -     0.005 x 12 = 0.06
What is 140% of 8?     -     1.4 x 8 = 11.2

Sept. 30, 2014 - Convert Fractions to Decimals to Percents

Tuesday, we added one more conversion, convert fractions to decimals and then to percents.  So what is a percent?  Percent is a comparison to 100.  We have already learned to convert a fraction to a decimal, divide the numerator by the denominator (top in bottom out).  To convert a terminating decimal to a fraction you say it correctly using place value and a repeating decimal you do the "9-Thing."

To convert a decimal to a percent you just move the decimal 2 places to the right and add a percent sign.

examples:
0.25 = 25%
1.5 = 150%

To convert a percent to a decimal you move the decimal 2 places to the left and take off the percent sign.

examples:
46% = 0.46
125% = 1.25

The hardest thing to remember is which way you move the decimal.  We think about Dr. Pepper to helps us remember.  Dr. Pepper means to change a decimal to a percent you move the decimal to the right D to P.  To convert a percent to a decimal you move the decimal to the left which is P to D.  You always move the decimal 2 places because there are 2 zeros on 100.

Students will have to give the missing values when given either the fraction, the decimal, or the percent.

    Fraction         Decimal            Percent   
      3/4                  .75                   75%  

     1  65/100        1.65                  165%  
     1  13/20  


        4/5                 0.8                   80%

Sept. 29, 2014 - Convert Decimals to Fractions

Monday, we learned to convert terminating and repeating decimals into fractions or mixed numbers.  First, let's have some definitions.

terminating decimals - decimals that stop. They do not repeat.  When dividing you have a remainder of 0.
examples:  0.25,  3.674

repeating decimals - decimals that repeat a number or series of numbers continually. To write a repeating decimal, you write the number or series of numbers that repeat one time and put a bar on top of the numbers that repeat.
                   __      __
examples:  0.5,   4.45

To convert a terminating decimal to a fraction you just say the decimal correctly using place value.

examples:
0.6 = 6/10 = 3/5
4.75 = 4  75/100 = 4  3/4

To convert a repeating decimal, where the entire decimal is repeating, you do what we call the "9-thing."
You put the decimal as the numerator and for each digit that is repeating in the decimal you put a 9 in the denominator.

examples:
  __
0.5 =    5/9
   __
0.63 =  63/99 = 7/11
   ___
5.363 = 5  363/999 = 5  121/333

Week of Sept. 29th

This week we will begin discussing percents.

Monday - We will change continue with last weeks information of converting fractions to decimals and convert terminating and repeating decimals where the entire decimal is repeating.

Tuesday - We will introduce percents and convert our fractions and decimals to percents.

Wednesday - We will learn to calculate percent of a number focusing on sales tax, tip, and discount.

Thursday and Friday - We will begin solving simple 1-step equations with addition, subtraction, multiplication, and division.

Bonus Question of the Week:

On a piece of paper, copy this problem down and work it.  Make sure you show all your work and that your answer has a correct label.  Turn it in by Thursday, Oct. 2nd for 10 Bonus points.

Ryan transfers 15% of his monthly pay into a savings account. If Max makes $1850 per month, how much will he save in a year?

Wednesday, Sept. 24, 2014

Today, we will change fractions to terminating and repeating decimals.  To change a fraction to a decimal you divide the numerator by the denominator.

                       .  6

                   _____

ex.  3/5 = 5 | 3 . 0            so 3/5 = 0.6

                   -3   0

                  ______

                          0

The .6 is a terminating decimal because it stops with a remainder of 0.

A repeating decimal is a decimal number that repeats a single digit or group of digits.

                   __

ex.  1/3 =  0.3

When you divide 1 by 3 the 3 repeats.  Once it repeats 3 times you can consider it to be a repeating decimal.  You write the number of group of numbers one time and put a bar on top of the number or group of numbers that repeat.

We will also receive in class a list of 41 fraction to decimal equivalents to divide.

Click here for a list of equivalents that I want you to memorize.

We will also introduce the calculator to help with converting fractions to decimals.

Week of Sept. 22nd

This week we will have our second test, Test 1-2.  This test will cover operations with integers, mixed numbers, and decimals.  We will review on Monday and then test on Tuesday.  We are also supposed to have our first Pep Rally on Tuesday which will possibly modify our afternoon class schedule.  If I feel the students will not have enough time to complete the test I may postpone it until Wednesday.  If that happens I will just flip Tuesday and Wednesday's schedule on my calendar.

Wednesday, we will convert fractions to terminating and repeating decimals.  The students will enjoy this day because we will also introduce the graphing calculators.  The students will also receive a list of 41 fraction to decimal equivalents that I will want them to memorize.  Don't worry, there is a trick to memorizing them.

Thursday, we will carry our fractions to decimals one step further, to percents.

Friday, we will begin finding percent of a number.  We will be looking at sales tax and discount to teach this lesson.  So next time you go shopping have your child figure what the sales tax might be on your purchase.

Bonus Question of the week:

The Rodriguez family went to dinner at Pasta Palace. Mr. Rodriguez ordered a meal for
$6.25; Mrs. R ordered a meal for $7.50; the 2 children ordered individual pizzas for
$4.99 each. The sales tax rate was 7.25% and they left a 15% tip. How much was the
total bill?

Copy the question, solve, and turn it in by Friday for 10 Bonus points.

Decimal Operations

Thursday and Friday we discussed decimal operations.  This is something that the students should be good at because they have been learning decimals since 4th and 5th grade.

Addition and Subtraction

-There is one thing to remember when adding and subtracting decimals:  line up the decimals.  Along with that add zeros as place holders and add or subtract you numbers.

-To multiply decimals you multiply the numbers as though the numbers do not have decimals.  Just line up your numbers and multiply.  To determine where the decimal goes you count the numbers to the right of the decimal in each number in the problem.  The sum is equal to the number of places you move the decimal to the left in your answer.

-To divide decimals you have to make sure your divisor (the number on the outside) is a whole number.  If it is not you move the decimal to the right until it is a whole number.  The number of places you moved the decimal in your divisor you move the decimal in your dividend, the number under the "house."  Once you have moved the decimal in both the divisor and dividend you bring the decimal to the top and divide.

(Images taken from Google Images)

Divide Fractions and Mixed Numbers

To divide fractions we first need to understand a reciprocal.  Reciprocals are two fractions, that when multiplied, equal 1.

Examples:

Fractions                 Reciprocals

     5 = 5/1                   1/5

     3/4                         4/3 = 1  1/3

     3  2/3 = 11/3          3/11

So you turn the number into a fraction if it is not already and then just flip it.

To help us remember how to divide fractions we learned a a little rap.

  To De-vide fractions

  Don't ask why

  Just flip the second

  And Multiply

  To Multiply fractions

  You know you've gottem

  It's top times top

  And Bottom times bottom.

If you would like to listen to the rap click here to here my class.

Here is an example of 

Multiplying Mixed Numbers

The past two days we have been learning to multiply positive and negative mixed numbers.  The students found this to be easier than expected.

To multiply mixed numbers you first must change each number in the problem to a fraction.  If you have a mixed number you use the "Popcorn Method" to change it to a fraction.

If the number is a whole number you just put a 1 as the denominator.  Once you have fractions you multiply the numerators together and then the denominators and simplify your answer.

In this example we simplified our answer by dividing 195 by 20.  The second way we simplified we looked for what 15 and 20 had in common and divided by the common factor.  The students learned that there is a 3rd way to simplify.  You can simplify the problem before you multiply.

Week of September 15th

This week in class we will finish mixed number operations and begin decimal operations.  The students did very well adding and subtracting positive and negative mixed numbers.  I was very pleased with how they performed.

Students will receive their 1st six weeks Progress Reports on Tuesday.  I realize some parents are used to the Parent Portal from the previous gradebook, hopefully, it will be available soon.

Math and Science teacher's will be trained on our new digital textbooks this next week.  So students should be getting information of the books soon as well.

Wednesday is Fall Picture day.

Bonus Problem for Students - worth 10 points

"The training session held 50 people. On Monday 38 people attended. On Wednesday 46  people attended. On Thursday only 1/2 as many as Wednesday's group attended. How many  people attended this week?"

To earn the 10 points you must write the question of a sheet of paper, answer the question with its correct label, and turn it in by Friday, Sept. 19th.

Add and Subtract Mixed Numbers

Wednesday we began adding and subtracting mixed numbers with a slight twist, negatives.  We began class by discussing what a fraction looks like.  I had the students draw a picture of 5/8. I noticed that the students, for the most part, understand the true meaning of what a fraction is.  Here are the 2 correct answers out of 3 that they gave me:

A fraction is a part to total relationship.  5/8 means it takes 8 pieces to make a whole and I have 5 of them.

Next, we review the steps to add and subtract fractions.

1.  Find a common denominator
2.  Change your numerator to match
3.  Add or subtract your numerators
4.  Keep your new denominator
5. SIMPLIFY!!!!!

Then we moved to mixed numbers.  We added one step when adding or subtracting mixed numbers and that was to add or subtract your whole parts.  I like putting that step between step 4 and 5.

At this point I told the students we are finally ready to begin our lesson which was to add or subtract mixed numbers with negatives.  We did this problem:

The students realized that you answer this question just like any other you just have to throw in your integer rules.

We will finish this lesson on Thursday.

Integer 4-Corner Model

Today, we began a small project.  Students are to create a 4-Corner Model with their integer rules.

In each section the students are to:

- Title the section (ex. Add Integers),

- In complete sentences, provide the rules to complete the operation,

- Give 2 examples of the operation.

In the center section, the students are to write a word problem using one of the operations.  The problem does not have to unique.  They can copy one from a previous assignment, find one in a textbook, or create one themselves.

Students can make this 4-Corner Model using paper like the image above, or they may choose their own medium, such as a Google Doc, Google Presentation, a Prezi, a Smore, etc. whatever they choose.

This project is due, if a paper copy, by the end of the day Thursday, Sept. 11.  If the project is digital they have until midnight Thursday.

Divide Integers

Today, we discussed the rules for division of integers.  The students found out that the rules for division are the same as the rules for multiplication.

There are 2 steps for dividing integers:
Step 1:  Divide your numbers
Step 2:  Count your negatives
   - If you have an even number of negatives your answer will be positive.
   - If you have an odd number of negatives your answer will be negative.

Examples:

24 / -4 = -6            -32 / -8 = 4

Tomorrow we will be working on a small project to help us better understand our integer rules.  Students will be able to create their project with regular paper, or they can create a digital presentation using Google, or a Prezi, or a Smore, etc.  More information will be provided in class tomorrow.

Week of Sept. 8 - 12

This week we will finish our lessons on Integers.  We will discuss division of integers on Monday.  We will find out that the rules for division will be the same as the rules for multiplication.  We will also get our test back from Friday.  The results were not bad but there is still much work to be done.

Tuesday, we will begin a small project to help us review the integer rules.

Wednesday, the students will be happy that we will not have anymore lessons on Integers but they will find our that the rules will still apply to positive and negative fractions and decimals.  We call these Rational Numbers.  So Wednesday, we will discuss add and subtracting fractions and mixed numbers.  This should be a review.  We will see.

Thursday, we will examine subtraction of mixed numbers where you have to borrow from the first mixed number.

Friday, we will begin a 2 day lesson on multiplication of mixed numbers.

Friday will also be the end of the first 3 week period of school.  Expect to see a progress report first of next week.

Test 1-1 Review

Today in class we completed a Test Review because tomorrow we will be taking our first test of the 2014-2015 school year.

The topics include:
-Writing an integer to represent a situation.
-Comparing and ordering a list of integers.
-Absolute value of a number
-Add, Subtract, and Multiply Integers

The students should have a copy of the test review with the correct answers, but if not here is a link to a blank review and here is a link to the answers to the review.

This question always comes up just before the first test of the year, "How do I study for a math test?"
Here are a couple of ideas:
- Print the review and try to work all the problems again.
- Read over your notes so that you can remember what they say without having to look at them.
- If there are rules to learn be able to quote them and apply them.
- Look back over old assignments. Work some of the problems we did not complete.

There are many ways to study besides these but this is a start.

Good luck on your test tomorrow.

Multiply Integers

Today we discussed the rules for multiplying integers.  We found out that to multiply integers we use two basic steps.

Step 1:  Multiply the numbers like you have in the past.  Pretend the numbers are all positive.

Step 2:  Count the number of negative signs in the problem.
     - If you have an even number of negative signs your answer will be a positive.
     - If you have an odd number of negative signs your answer will be a negative.

Examples:

6 x 3 = 18

-5 x 3 = -15        There is 1 negative so the answer is negative.

-7 x -4 = 28         There is 1 negative so the answer is negative.

-2 x 3 x -2 = 12          There are 2 negatives so the answer is positive.

-5 x -2 x -2 = -20        There are 3 negatives so your answer is negative.

-1 x -1 x -1 x -1 x -1 x -1 x -1 = -1         There are 7 negative signs so the answer is negative.

If you need additional instruction click here.

Subtract Integers

Today we discussed the procedure to subtract integers.  Ex.  15 - (-21) =  We determined that to subtract integers you really have to add.

We use a process of LCO+ to work a subtraction of integers problem.  LCO+ stands for:

L - leave the first number alone
C - change the subtraction sign to an addition sign
O - change the next number, after the subtraction sign, to its opposite
+ - revert back to your addition rules because the problem is now addition

Ex.  15 - (-21) =

       15 + 21 = 36

The 15 stayed the same.  We changed the - sign to +, and the 21 changed from negative to positive.  The signs of the new problem are alike so we add them together.

Additional examples:

Ex.   -6 - (-8) =                               -9 - 7 =

        -6 + 8 =  2                              -9 + (-7) = -16

Friday - Addition of Integers

Friday we began discussing one of the most important topics we will learn all year, integer operations.  We will learn how to add, subtract, multiply, and divide integers which are the set of whole numbers and their opposites.  Friday we learned about addition of integers.

Students need to remember the following process:
- If your signs are alike you add your numbers and keep the sign of the problem.
     ex.  5 + 8 = 13          -6 + (-5) = -11

- If your signs are different you subtract your numbers and take the sign of the number with the greatest absolute value (the distance the number is from 0).
     ex. -6 + 3 = -3           9 + (-15) = -6

If you need additional help click here.

Here is a .pdf file of my lesson on addition of integers.

Number Sets

Today in class we discussed types of numbers such as natural numbers, whole numbers, integers, rational and irrational numbers, real numbers, imaginary and complex numbers.  By the end of class the students were asked to place individual numbers into their proper set.  The students did a great job.  Below is a graphic we used in class to help the students understand how all the sets are connected.

Click on the link below if you want to learn more about number sets.

http://www.mathsisfun.com/sets/number-types.html

Pre-Test

Today we took a Pre-Test over Computation skills.  Most students seemed to do ok with whole numbers, and add and subtract decimals, but fractions and integers we need some work.  Good thing integers will be our topic of conversation for the next few days.

Tomorrow, we will discuss sets of numbers like counting numbers, whole numbers, integers, rational and irrational numbers, real numbers, imaginary numbers, and complex numbers.

First Day

The first day of school went pretty well.  I was pleased with how things went.  Today we find out how much the students remember about math.  Good luck on the Pre-Test.

Monday at Mance Park

I hope all the students are ready for Monday.  Students will report to their grade level gym, get a copy of their class schedule, and at about 7:40 be released to go to their 1st period class.  7th graders will go to a general assembly during 1st period to discuss policies and procedures with our Principal, Mr. Bennett.  8th grade will do the same thing during their 2nd period class.  When not in the assembly during 1st through 4th periods you will discuss topics in the Mance Park handbook.  During 5th through 7th periods teachers get to begin class.

Here is a look at your Principals.  From left to right you have Mr. Dunbar, AP for 8th Grade, Mr. Bennett, Principal, and Mr. Spencer, AP for 7th grade.

Meet and Greet

I want to thank all the parents for coming to the 7th grade Meet and Greet at Mance Park Middle School.  The turnout was great.  I look forward to working with each of you during this upcoming school year.

We will begin the year with Integers.  Watch this short video if you would like a preview.

https://www.youtube.com/watch?v=7zXlT1GtWTU

Welcome

Welcome to Mr. Nash's 7th Grade PreAP Math class.  You will learn many new things this year.  Come ready to learn.

The best way to contact me is through email.  I check my email frequently so I will try to get back to you as soon as I can.  You may send text messages to my Google Voice mail, but I keep it on silent so I don't check it as frequently.  I typically will not respond after 9:00pm or before 6:00am.

Contact information:
email:  jnash@huntsville-isd.org
School Phone Number:  936.293.2755
Google Voice mail:  936.755.3198